Déroulement de la séquence

Déroulement de la séquence

A faire avant à la maison :

exercice 5 du notebook NSI Récursivité (1/2) : notions de fonctions

A faire en classe :

Le professeur corrige l’exercice qui devait être fait à la maison et refait un bilan global de ce qui a été vu dans le notebook précédent.

Il donne ensuite le notebook NSI Récursivité (2/2) : notions de récursivité que les élèves auront à traiter en autonomie. Le professeur passe dans les rangs pour vérifier l’avancée des travaux, répondre aux questions et donner des conseils. Il n’hésitera pas à faire des points bilans régulièrement (par exemple à la fin de chaque exercice)

Cette seconde activité a pour but de manipuler quelques exemples classiques liées à la récursivité et d’en dégager quelques notions importantes.

Elle est composée de cinq exercices progressifs permettant de comprendre la notion d’appels récursifs, la problématique des cas de base et la notion de pile d’appels.

Exercice 1 : factorielle d’un entier naturel

Le but de ce premier exercice est de faire comprendre aux élèves la notion d’appels récursifs sur un exemple très simple.

Après un rappel de la définition de la factorielle et de sa propriété fondamentale $n! = n\times(n-1)!$ , on demande aux élèves de compléter le code suivant :

Figure 1 : code de la fonction `fact` à compléter

On pourra revenir avec les élèves sur la notion d’assertion. Ici, il s’agit de voir si les élèves sont capables de restranscrire la propriété fondamentale de la factorielle sous la forme d’un code informatique, la notion de récursivité étant intrinsèque à la définition de la factorielle.

Un jeu de tests (figure 2) est proposé aux élèves :

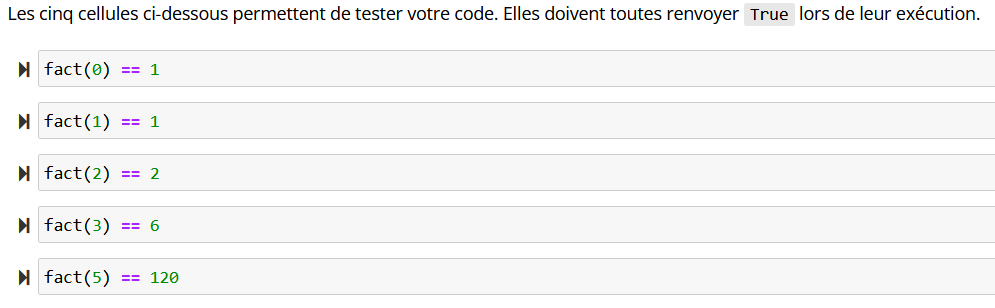
Figure 2 : jeu de tests pour la fonction `fact`

Une fois le code complété et les tests passés, on demande aux élèves d’expliquer à la main les différents appels qui ont lieu lors de l’exécution de l’instruction fact(4). Dans un second temps, ils vérifient leur réponse à l’aide de l’outil RecursionVizualizer (figure 3).

Figure 3 : exécution de `fact(4)` avec RecursionVizualizer

Exercice 2 : appels infinis ?

On s’intéresse ici à la notion de cas de base et à la notion de fonctions récursives bien formées.

On considère dans un premier temps le code de la fonction mystère suivant :

Figure 1 : code de la fonction `mystère`

En utilisant l’outil RecursionVisualizer, les élèves doivent répondre aux deux questions suivantes : que renvoie l’instruction mystère(2) et comment sont effectués les différents appels récursifs ? Il s’agit ici de réinvestir ce qui a été vu dans le premier exercice.

Dans un second temps, on modifie la fonction mystère en la fonction mystère_infini comme suit :

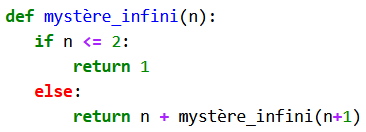
Figure 2 : code de la fonction `mystère_infini`

et on demande aux élèves ce que renvoient les deux instructions mystère_infini(2) et mystère_infini(3). Pour la seconde instruction, on propose aux élèves de s’aider des deux outils de visualisation Python Tutor et RecursionVizualiser. Il s’agit ici de bien faire comprendre aux élèves l’intérêt du cas de base dans une fonction récursive et de faire la distinction entre fonctions récursives et fonctions récursives bien formées.

Exercice 3 : suite récurrente

Dans cet exercice, on considère la suite récurrente :

{\begin{cases} u_{n + 1} = 3 u_{n} + 1 \\ u_{0} = 12 \end{cases}

$\begin{cases}u_{n+1}=3u_n+1\\u_0=12\end{cases}$

Il s’agit ici d’écrire deux programmes informatiques permettant d’évaluer le terme de rang $n$ de la suite $(u_n)$ .

Dans un premier temps, on demande aux élèves de compléter un code itératif pour répondre à ce problème (figure 1). Il s’agit ici de revoir quelques notions classiques sur les boucles.

Comme dans l’exercice 1, un jeu de tests (figure 2) est proposé aux élèves :

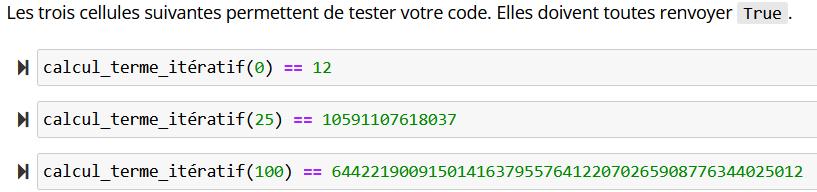
Figure 2 : jeu de tests pour la fonction `calcul_terme_itératif`

Dans un second temps, on demande aux élèves d’écrire, à l’aide de l’outil Code Puzzle (figure 3), un code récursif pour répondre au problème :

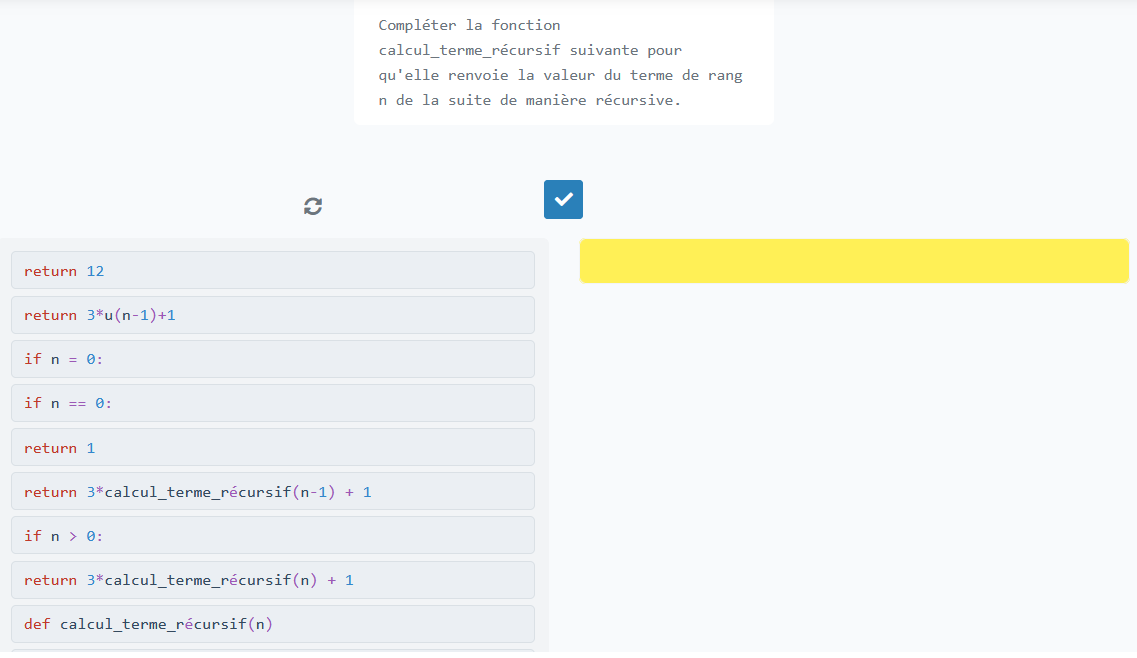
Figure 3 : code récursif à écrire dans Code Puzzle

Il s’agit ici, pour les élèves, du premier code récursif à écrire entièrement. Un des intérêts d’utiliser Code Puzzle pour cet exercice est de pouvoir proposer des éléments syntaxiques tout fait, sans qu’ils ne soient toutefois déjà disposés dans l’ordre comme un simple code à compléter, ainsi que des éléments distracteurs. Ceci impose donc aux élèves d’avoir bien compris en amont les notions de cas de base et d’appels récursifs. Le professeur pourra passer ici un peu de temps pour revoir avec les élèves l’écriture d’un code récursif et insister à nouveau sur les notions de cas de bases et d’appels récursifs.

Exercice 4 : calcul de carrés

Le but de cet exercice est d’amener les élèves à écrire un code récursif répondant à un problème donné en cherchant où se situe précisément l’appel récursif. Plus précisément, on s’intéresse au calcul récursif d’un carré d’entier naturel qui est analogue au calcul de la factorielle de l’exercice 1.

Dans un premier temps, après avoir rappelé l’identité remarquable $(n+1)^2=n^2+2n+1$ , on demande aux élèves d’établir une relation entre $n^2$ et $(n-1)^2$ .

Pour une meilleure compréhension, le professeur peut écrire la relation précédente en utilisant explicitement la fonction carré carré(n+1)= carré(n)+ 2*n + 1

Une fois la relation établie, on demande aux élèves de compléter le code suivant (figure 1) pour lequel un jeu de tests est proposé (figure 2) :

Figure 1 : code de la fonction `carre` à compléter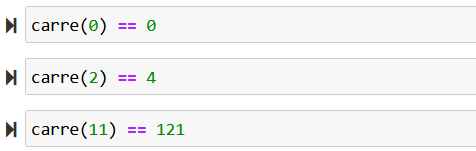

Figure 2 : jeu de tests pour la fonction `carre`

Une fois le code complété et les tests passés, on réinvestit ce qui a été vu dans l’exercice 1 en demandant aux élèves d’expliquer à la main les différents appels qui ont lieu lors de l’exécution de l’instruction carre(4), puis de vérifier leur réponse à l’aide de l’outil RecursionVizualizer.

A faire après à la maison :

Exercice 5 : maximum dans une liste

Dans cet exercice, on propose un code récursif pour déterminer le maximum dans une liste.

Après avoir proposé un algorithme, on demande aux élèves de justifier que celui-ci induit un algorithme récursif.

On donne ensuite la fonction suivante qui permet d’implémenter cet algorithme, tous les rappels nécessaires sur le slicing étant donnés aux élèves :

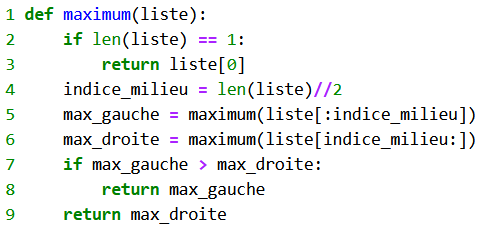
Figure 1 : implémentation de l'algorithme récursif

On demande aux élèves d’indiquer les lignes correspondant aux trois étapes de l’algorithme : cas de base, découpage en sous-listes et combinaison des résultats.

On s’intéresse ensuite à la gestion des différents appels récursifs et notamment à l’ordre dans lequel sont obtenus les différents calculs intermédiaires des maximums (gestion du cas de base pour une liste de longueur 1, ou gestion des deux maxima pour une liste de longueur supérieure ou égal à 2). Pour se faire, les élèves utilisent RecursionVizualiser pour les aider à décrire cette gestion. Ils utilisent ensuite Python Tutor pour interpréter du point de vue de la machine ces différents appels, ce qui permet d’introduire la notion de pile d’exécution.

A faire en classe la fois suivante :

Correction de l’exercice 5 puis bilan avec les élèves avec un retour sur les notions fondamentales de la récursivité : cas de base, appels récursifs, pile d’exécution. Réinsister également sur la différence entre fonctions récursives et fonctions récursives bien formées.